Wenn die meisten von uns eine Taffy-Pulling-Maschine auf einer touristischen Promenade vorbeikommen sehen, denken wir an süßen, süßen Zucker. Jean-Luc Thiffeault denkt an süße, süße Mathematik. Als angewandter Mathematiker an der Universität von Wisconsin-Madison interessiert sich Thiffeault besonders für die Art und Weise, wie Materialien wie Taffy gemischt werden: In der Maschine wird die Süßigkeit gedehnt und gefaltet, um Luft aufzunehmen und ihre leichte, zähe Textur zu entwickeln. Wenn es gezogen wird, wird das ursprüngliche Rechteck des Taffys immer mehr gedehnt - seine Länge wächst jedes Mal exponentiell um das gleiche Verhältnis. Dieses Streckverhältnis interessiert Thiffeault.
Verwandte Inhalte
- Schmelzfeste Schokolade, 3D-bedruckte Gummis und andere faszinierende Bonbonpatente
Wenn eine Person Toffee zieht, nimmt sie im Allgemeinen den Bonbonklumpen und streckt ihn über einen Haken, wodurch die beiden Enden zusammengeführt werden. Dann werden sie das gefaltete Stück nehmen und es wieder über den Haken spannen, die Länge verdoppeln und so weiter. Mit anderen Worten: „Die menschliche Art, dies zu tun, ist ein Multiplikationsfaktor von 2“, sagt Thiffeault. Mechanische Abzieher können es besser machen und ergeben oft größere, exotische irrationale Zahlen als ihre Dehnungsfaktoren.
Es stellt sich heraus, dass Taffy Pulling durch ein abstraktes Gebiet der Mathematik modelliert werden kann, das als topologische Dynamik bezeichnet wird. Dabei handelt es sich im Wesentlichen um das Studium langfristiger, großräumiger zeitlicher Veränderungen in einem mathematischen Raum. (Wenn das Wort Topologie bekannt vorkommt, wurde es kürzlich im Rahmen des diesjährigen Nobelpreises für Physik in den Nachrichten erwähnt.) Die gleiche Mathematik, die das Taffy-Pulling beschreibt, hat auch ernstere Anwendungen: Viele industrielle Prozesse, einschließlich Glasbläserei und Arzneimittelherstellung, erfordern viskose Flüssigkeiten, die auf eine Weise gemischt werden, die eher dem Ziehen von Toffee gleicht, als dem Einrühren von Sahne in Kaffee. "Wenn Sie versuchen, wirklich viskose Dinge wie Pasten für die Pharmaindustrie zu rühren, können Sie sie nicht einfach schütteln", sagt Thiffeault. "Es ist nicht wie Mischen von Farbe."
Thiffeault hat Taffy-Pulling lange Zeit als Beispiel für viskoses Mischen verstanden, aber erst vor kurzem hat er sich mit der Geschichte der Taffy-Puller befasst, um ihre mathematischen Geheimnisse zu entdecken. Das Ergebnis dieser Exkursion in historische Patente ist sein kürzlich veröffentlichter Aufsatz „Eine mathematische Geschichte von Taffy Pullern“, der im Juli auf dem Preprint-Server arXiv veröffentlicht wurde.
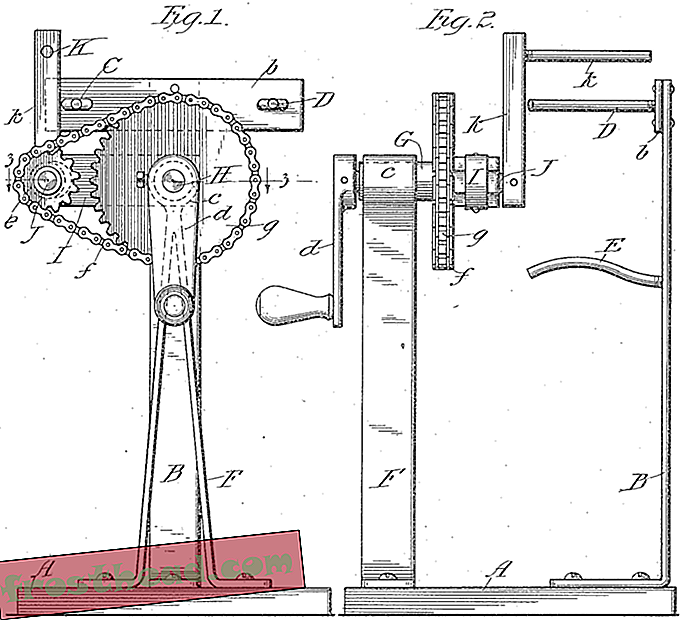 Ein Bild von einem 1916 Taffy-Maschine-Patent, das in Thiffeaults Studie erscheint.
Ein Bild von einem 1916 Taffy-Maschine-Patent, das in Thiffeaults Studie erscheint. Das Gebiet, das zu seinem tiefen Abtauchen führte, ist das Studium von sogenannten Pseudo-Anosov-Mappings. Pseudo-Anosov ist eine ausgefallene Methode zur Beschreibung eines Prozesses, bei dem eine zweidimensionale Form exponentiell in eine Richtung gedehnt wird, während sie in der anderen schrumpft. Mathematisch ist das Studium von Pseudo-Anosov-Abbildungen relativ neu. "In den 70er und 80er Jahren haben die Leute sehr hart nach Beispielen gesucht", sagt Thiffeault. Ironischerweise waren sie die ganze Zeit in Patenten für Taffy-Puller dabei. "Weil sich Mathematiker diese Literatur nie angesehen haben, hätten sie nie gewusst, dass es sie gibt", sagt er.
Während er Patente durchforstete, stieß Thiffeault auf einen Rechtsstreit, der bis zum Obersten Gerichtshof führte. In der Rechtssache Hildreth v. Mastoras von 1921 ging es darum, wie weit ein Patent von 1900 für einen Taffy-Puller ausgelegt werden sollte. Das heißt: War ein späteres Modell, das von jemand anderem hergestellt wurde, nur eine geringfügige Verbesserung, oder war es ein anderes Gerät? Ein entscheidender Teil des Arguments war, wie unterschiedlich das Patent von 1900 von einem Vorgänger von 1893 war (der wahrscheinlich nie hergestellt wurde). Die Meinung des Gerichts, verfasst von Richter William Howard Taft, "zeigt ein scharfes Verständnis der topologischen Dynamik", schreibt Thiffeault in seinem Artikel.
Das Gericht stellte fest, dass das frühere Gerät - das nur zwei Haken hatte - den Toffee nicht in dem für eine effiziente Herstellung von Konfekt erforderlichen Maße hätte dehnen können. Tafts Meinung besagt:
Mit nur zwei Haken konnte das Bonbon nicht geläppt werden, da es keinen dritten Stift gab, um das Bonbon wieder in Eingriff zu bringen, während es zwischen den anderen beiden Stiften gehalten wurde. Die Bewegung der beiden Stifte in konzentrischen Kreisen könnte es etwas dehnen und umrühren, aber es würde es nicht im Sinne des Standes der Technik ziehen.
Thiffeault schreibt: "Die Stellungnahme des Obersten Gerichtshofs zeigt die grundlegende Einsicht, dass mindestens drei Stäbe erforderlich sind, um ein schnelles Wachstum zu erzielen."
Laut Thiffeault sind heute zwei Standard-Taffy-Puller im Einsatz, einer mit drei Stangen und einer mit vier. Sie haben zufällig den gleichen Dehnungsfaktor. Es ist verwandt mit dem sogenannten Silberverhältnis, 1+ √2, oder etwa 2, 414, einem etwas weniger leuchtenden Verwandten des bekannteren Goldenen Schnitts.
Interessant ist, dass sich die beiden Standard-Taffy-Puller mit dem Silberanteil dehnen, da der Silberanteil - mathematisch gesehen - optimal ist. Thiffeault warnt jedoch davor, dass es nicht so einfach ist, verschiedene Taffy-Puller zu klassifizieren, selbst wenn man deren Dehnungsfaktoren kennt: „Es gibt einen Aspekt mit Äpfeln und Orangen, der ziemlich schwer zu umgehen ist“, sagt er. Ein Abzieher hat möglicherweise mehr Stangen und es dauert länger, bis er in den Ausgangszustand zurückkehrt, oder er erfordert möglicherweise mehr Drehmoment oder ein komplizierteres Getriebe. Die Mathematik gibt zwar einen Einblick darüber, wie gut Taffy-Puller ziehen, erzählt aber nicht die ganze Geschichte.
Thiffeaults Forschungen zu Taffy-Pullern inspirierten ihn und seinen Studenten Alex Flanagan, ein eigenes Modell zu bauen. Sie wollten herausfinden, ob sie den Wirkungsgrad steigern können, ohne die Getriebe stark zu verändern, und stellten schließlich einen neuartigen 6-Stangen-Abzieher her, der auf dem Getriebe des Standard-4-Stangen-Abziehers basiert. "Der Grund, warum wir es geschafft haben, ist, dass wir jetzt Mathe haben", sagt Thiffeault. Sie konnten die Maschine ausgiebig am Computer modellieren und einen Großteil des Versuchs und Irrtums mit realen physischen Geräten umgehen, die frühere Erfinder zu tun hatten. Das 6-Stangen-Gerät, bei dem es sich noch um einen Prototyp handelt, ist in jedem Zyklus etwa doppelt so lang wie die Standard-Abzieher.
Bisher haben Taffy-Puller-Hersteller Thiffeaults Tür nicht genau eingeschlagen, um seinen Rat zur Optimierung ihrer Designs einzuholen - Big Taffy ist anscheinend zufrieden mit seinem dehnbaren Status quo -, aber er hofft, dass seine Methoden Auswirkungen auf andere Branchen haben könnten. Ein logischer Ort für die Mischoptimierung ist neben dem Glasblasen die Pharmaindustrie. Denn das Mischen von Vitaminen und Medikamenten erfordert eine extrem hohe Qualitätskontrolle: Die Hersteller sind "bereit, viel Geld für das perfekte Mischen zu zahlen", weil sie "kein schlechtes Multivitamin von 1000 tolerieren können", sagt Thiffeault. Also, eines Tages, Apotheker geben vielleicht einen süßen Gruß an die ergebenen Taffy-Puller von früher.
Andererseits könnte das ein bisschen langwierig sein.